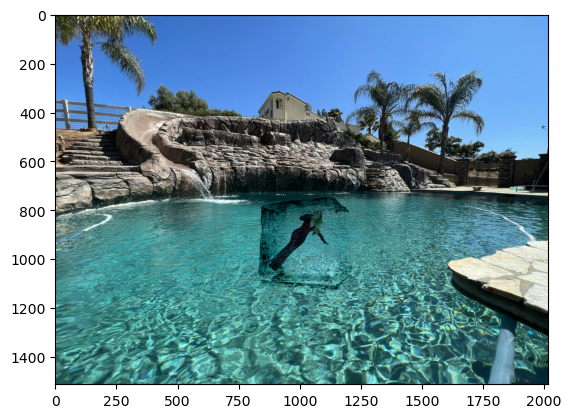
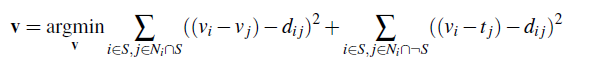Final Projects
Lightfield Camera and Gradient Domain Fusion
Depth Refocusing
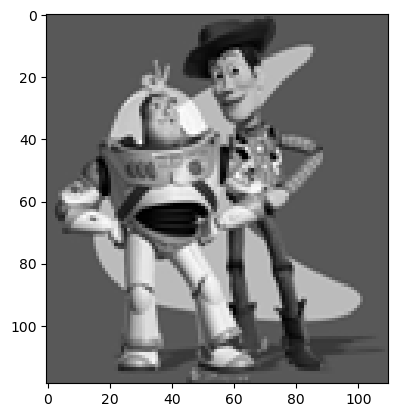
I use images from the Stanford Light Field Archive. There are 289 images of a chessboard and 289 images of an amethyst that form a "grid" of the same object at slightly different locations. (x, y) refers to an image relative to their position in the 17x17 grid. To refocus an image, I shift each image by c * (x - center_x) and -1 * c * (y - center_y). c represents the depth, so as c changes, the depth and therefore the focus of the image changes. center_x and center_y are the centers of the image grid. Because both grids are 17x17, the center images are both (8, 8).
As c increases, the focus of the image shifts downwards.
Aperture Adjustment
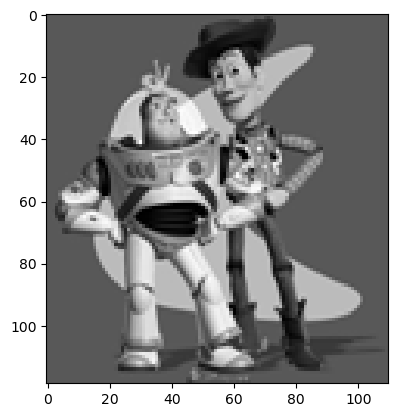
We can also mimic the object being taken with different apertures by applying the same formula as above, but skipping images that are more than aperature_size further from the center image. As the aperature increases, less images are skipped and the image becomes more blurry. However, the focus of the image remains the same as aperture changes. For both images, I used a c of 1.5.
Lightfield Camera Summary
Overall, it was really cool to see how effects of a camera could be mimicked by translation. I did not know the idea that objects closer to the camera moving less than objects further from the camera when the camera moves could be used to refocus images and change apertures.
Gradient Domain Fusion
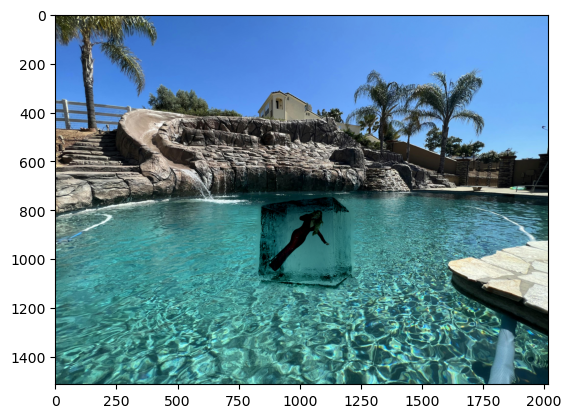
For this project, I use Poisson Blending and Mixed Gradients to blend an object into a background image seemlessly. Poisson blending matches the gradients (differences between neighboring pixels) of the source object inside a mask while ensuring smooth transitions at the mask boundary using the target image's pixel values.
Toy Problem
Before implementing Poisson blending, I first attempt to reconstruct a toy image using a similar algorithm. Essentially, I create the sparse matrix A such that using least squares to minimize ||Av - s||^2 allows us to minimize (v(x+1,y)-v(x,y) - (s(x+1,y)-s(x,y)))^2, minimize (v(x,y+1)-v(x,y) - (s(x,y+1)-s(x,y)))^2, and minimize (v(0,0)-s(0,0))^2.
Note: v is the flattened reconstructed image and s is the flattened original toy image.
Poisson Blending
Poisson Blending essentially just tries to minimize this equation:
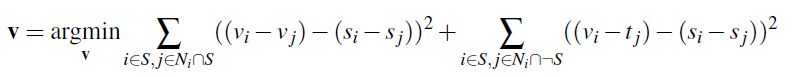
v is the resulting image, s is the flattened source image, and t is the flattened target image that we are blending s into.
S is pixels within the mask and N_i are the four pixels adjacent to i
The left part of the equation tries to minimze the gradients between the source image inside the mask and v. The right part of the equation sets v_j to t if v_j is outside the mask.
Similar to the toy problem, I create a sparse matrix A by looping through s. If the pixel in s falls in the mask, I loop through the four neighboring pixels, and if the neighboring pixels fall outside the mask, I set the corresponding values in b to include the pixel values from the target image at those positions. If the neighboring pixels are inside the mask, I update A to relate the current pixel and its neighbors. This ensures that gradients within the mask match the source image, while gradients at the boundary smoothly transition into the target image.
Mixed Gradients
I also implement Mixed Gradients, which is the same as Poisson Blending, but chooses, for each pixel pair, the gradient with the larger magnitude between the source and the target:
Overall, the images blended with mixed gradients are a little more seemless, as the edges between the source object and the target is a little less fuzzy. However, the source image is more transparent, which is especially noticeable in the image with Aang flying down the mountain.